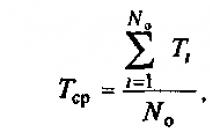Песенка, сочинённая английским студентом Чем больше учишься, тем больше знаешь. Чем больше знаешь, тем больше забываешь. Чем больше забываешь, тем меньше знаешь. Чем меньше знаешь, тем меньше забываешь. Но чем меньше забываешь, тем больше знаешь. Так для чего учиться? Не философия, а мечта лентяев!

Цель: изучить данную тему и создать презентацию для использования ее на уроках. Задачи: 1. Дать определение понятиям «софизм» и «парадоксы»; узнать, в чем их отличие. 2. Классифицировать различные виды софизмов и парадоксов. 3. Понять, как найти в них ошибку. 4. Составить компьютерную презентацию

Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. Особенно часто в софизмах выполняют "запрещенные" действия или не учитываются условия применимости теорем, формул и правил. Математические софизмы Софизм- формально кажущееся правильным, но по существу ложное умозаключение, основанное на неправильном подборе исходных положений (словарь Ожегова)

Парадокс (греч. "пара" - "против", "доска" - "мнение") близок к софизму. Но от него он отличается тем, что это не преднамеренно полученный противоречивый результат.софизму Парадокс - странное, расходящееся с общепринятым мнением, высказывание, а также мнение, противоречащее (иногда только на первый взгляд) здравому смыслу (словарь Ожегова). Математический парадокс – высказывание, которое может быть доказано и как истинна, и как ложь. Парадоксы Парадоксы

В Греции софистами называли и простых ораторов - философов - учителей, задачей которых было научить своих учеников « мыслить, говорить и делать ». Их задачей обычно было научить убедительно защитить любую точку зрения. Парадоксы были типичными способами постановки вопроса в античном мышлении. За свою историю математика испытала три сильнейших потрясения, три кризиса, которые касались ее основ. И все три сопровождались обнаружением парадоксов. А теперь немного истории…

« Два неодинаковых натуральных числа равны между собой » решим систему двух уравнений Сделаем это подстановкой у из 2- го уравнения в 1, получаем х +8- х =6, откуда 8=6 Где ошибка Уравнение (2) можно записать как х +2 у =8, так что исходная система запишется в виде: Х +2 у =6, Х +2 у =8 В этой системе уравнений коэффициенты при переменных одинаковы, а правые части не равны между собой, из этого следует, что система несовместна, т. е. не имеет ни одного решения. Графически это означает, что прямые у =3- х /2 и у =4- х /2 параллельны и не совпадают. Перед тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли система единственное решение, бесконечно много решений или не имеет решений вообще.

« Уравнение x-a=0 не имеет корней » « Уравнение x-a=0 не имеет корней » Дано уравнение x-a=0. Разделив обе части этого уравнения на x-a, получим, что 1=0. Поскольку это равенство неверное, то это означает, что исходное уравнение не имеет корней. Где ошибка? Поскольку x=a – корень уравнения, то, разделив на выражение x-a обе его части, мы потеряли этот корень и поэтому получили неверное равенство 1=0.

0, что: a + c = b умножим обе части на (a b), имеем: (a + c)(a b) = b(a b) a 2 + ca ab cb = ba b 2 cb переносим вправо, имеем: a 2 + c" title="« Все числа равны между собой » « Все числа равны между собой ». возьмём числа a 0, что: a + c = b умножим обе части на (a b), имеем: (a + c)(a b) = b(a b) a 2 + ca ab cb = ba b 2 cb переносим вправо, имеем: a 2 + c" class="link_thumb"> 12 « Все числа равны между собой » « Все числа равны между собой ». возьмём числа a 0, что: a + c = b умножим обе части на (a b), имеем: (a + c)(a b) = b(a b) a 2 + ca ab cb = ba b 2 cb переносим вправо, имеем: a 2 + ca ab = ba b 2 + cb a(a + c b) = b(a b + c) отсюда a = b Где ошибка? По определению: a + c = b Значит, a + c b = 0 И выражение a(a + c b) = b(a + c b) Тождественно a 0 = b 0. 0, что: a + c = b умножим обе части на (a b), имеем: (a + c)(a b) = b(a b) a 2 + ca ab cb = ba b 2 cb переносим вправо, имеем: a 2 + c"> 0, что: a + c = b умножим обе части на (a b), имеем: (a + c)(a b) = b(a b) a 2 + ca ab cb = ba b 2 cb переносим вправо, имеем: a 2 + ca ab = ba b 2 + cb a(a + c b) = b(a b + c) отсюда a = b Где ошибка? По определению: a + c = b Значит, a + c b = 0 И выражение a(a + c b) = b(a + c b) Тождественно a 0 = b 0."> 0, что: a + c = b умножим обе части на (a b), имеем: (a + c)(a b) = b(a b) a 2 + ca ab cb = ba b 2 cb переносим вправо, имеем: a 2 + c" title="« Все числа равны между собой » « Все числа равны между собой ». возьмём числа a 0, что: a + c = b умножим обе части на (a b), имеем: (a + c)(a b) = b(a b) a 2 + ca ab cb = ba b 2 cb переносим вправо, имеем: a 2 + c"> title="« Все числа равны между собой » « Все числа равны между собой ». возьмём числа a 0, что: a + c = b умножим обе части на (a b), имеем: (a + c)(a b) = b(a b) a 2 + ca ab cb = ba b 2 cb переносим вправо, имеем: a 2 + c">

Арифметика - (греч. arithmetika, от arithmys число), наука о числах, в первую очередь о натуральных (целых положительных) числах и (рациональных) дробях, и действиях над ними. Так что же такое арифметические софизмы? Арифметические софизмы – это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.

« Дважды два - пять » Напишем тождество 4:4=5:5. Вынесем из каждой части тождества общие множители за скобки, получаем: 4(1:1)=5(1:1) или Так как 1:1=1, то сократим и получим Где ошибка? Ошибка сделана при вынесении общих множителей 4 из левой части и 5 из правой. Действительно, 4:4=1:1, но 4:44(1:1).

« Пять равно шести » Возьмем тождество = В каждой части вынесем за скобки общий множитель: 5(7+2-9)=6(7+2-9). Теперь, получим, что 5=6. Где ошибка? Ошибка допущена при делении верного равенства 5(7+2-9)=6(7+2-9) на число 7+2-9, равное 0. Этого нельзя делать. Любое равенство можно делить только на число, отличное от 0.

« Один рубль не равен ста копейкам » « Один рубль не равен ста копейкам » Известно, что любые два равенства можно перемножить почленноее, не нарушая при этом равенства, т. е. если а = b и c = d, то ac = bd. Применим это положение к двум очевидным равенствам: 1 рубль = 100 копейкам и 10 рублей = 1000 копеек Перемножая эти равенства почленноее, получим 10 рублей = копеек и разделив последнее равенство на 10, получим, что 1 рубль = копеек Таким образом, один рубль не равен ста копейкам.

Парадокс « Разность квадратов » Парадокс « Разность квадратов » 1) а²-а² = а²-а² - имеем равенство 2) а(а-а) = (а+а)(а-а) – в первой части вынесем общий множитель за скобки, а во второй воспользуемся формулой 3) а = а+а – сократим на общий множитель (а-а) 4) а = 2 а.

Анкетирование 1. Укажите ваш пол. 2. Знакомы ли вам понятия математический « софизм » и « парадокс »? 3. Если, отвечая на предыдущий вопрос, вы ответили положительно, постарайтесь дать определения этих понятий. 4. Приводились ли примеры софизмов и парадоксов на уроках математики? (Ответ при условии положительного ответа на предыдущий вопрос) 5. Хотели бы вы больше узнать о математических парадосках и софизмах?

Заключение Я познакомился с увлекательной темой, узнал много нового, научился решать задачки на софизмы, находить в них ошибку, разбираться в парадосках. Тема моей работы далеко не исчерпана. Я рассмотрел лишь некоторые, самые известные примеры софизмов и парадоксов. На самом деле их намного больше. Развитая логика мышления поможет не только в решении каких - нибудь математических задач, но еще может пригодиться в жизни.

Литература 1. Lietzman W. Wo steckt der Fehler? Mathematische Trugschlüsse und Warnzeichen. – Leipzig? Аменицкий Н. Математические развлечения и любопытные приемы мышления. – М., Богомолов С. А. Актуальная бесконечность. – М.; Л., Больцано Б. Парадоксы бесконечного. – Одесса, Брадис В. М., Харчева А. К. Ошибки в математических рассуждениях. – М., Горячев Д. Н., Воронец А. М. Задачи, вопросы и софизмы для любителей математики. – М., Литцман В., Трир Ф. Где ошибка? – СПб., Лямин А. А. Математические парадоксы и интересные задачи. – М., Мадера А. Г., Мадера Д. А. Математические софизмы. – М.: Просвещение, Обреимов В. И. Математические софизмы. – 2- е изд. – СПб., 1889.

Title="Пример 10.Из двух неравных чисел первое всегда больше второго Пусть a и b – произвольные числа и a ≠ b. Имеем:(a – b)2 > 0, т.е. a2 – 2ab – b2 > 0, или a2 + b2 > 2ab.К обеим частям этого неравенства прибавим – 2b2. Получим:a2 – b2 > 2ab – 2b2, или (">

1 из 23

Презентация на тему: Математические софизмы

№ слайда 1

Описание слайда:

№ слайда 2

Описание слайда:

Что такое софизм? Правильно понятая ошибка – это путь к открытиюИ.П. Павлов Софизм (от греч. sophisma – уловка, выдумка, головоломка), формально кажущееся правильным, но по существу ложное умозаключение, основанное на преднамеренно неправильном подборе исходных положений. Каков бы ни был софизм, он обязательно содержит одну или несколько замаскированных ошибок. Особенно часто в математических софизмах выполняются «запрещённые» действия или не учитываются условия применимости теорем, формул и правил. Иногда рассуждения ведутся с использованием ошибочного чертежа или опираются на приводящие к ошибочным заключениям «очевидности». Встречаются софизмы, содержащие и другие ошибки.

№ слайда 3

Описание слайда:

В истории развития математики софизмы играли существенную роль. Они способствовали повышению строгости математических рассуждений и содействовали более глубокому уяснению понятий и методов математики. Роль софизмов в развитии математики сходна с той ролью, какую играют непреднамеренные ошибки в математических исследованиях, допускаемые даже выдающимися математиками. Именно уяснение ошибок в математических рассуждениях часто содействовало развитию математики. Пожалуй, особенно поучительна в этом отношении история аксиомы Евклида о параллельных прямых. Сформулировать эту аксиому можно так: через данную точку, лежащую вне данной прямой, можно провести не более одной прямой, параллельной данной (что одну прямую, параллельную данной, можно провести – это доказывается). Это утверждение на протяжении более чем двух тысяч лет пытались доказать, вывеси из остальных аксиом геометрии, но все попытки не увенчались успехом. Полученные «доказательства» оказались ошибочными. И всё же, несмотря на ошибочность этих «доказательств», они принесли большую пользу развитию геометрии. Можно сказать, что они подготовили одно из величайших достижений в области геометрии и всей математики – создание неевклидовой геометрии. Честь разработки новой геометрии принадлежит нашему великому соотечественнику Н.И. Лобачевскому и венгерскому математику Яношу Бойяи. Н.И. Лобачевский и сам сначала пытался доказать аксиому параллельных, но скоро понял, что этого сделать нельзя. И путь, идя которым Лобачевский убедился в этом, привёл его к созданию новой геометрии. Этот замечательный вклад в математику был одним из тех, которые прославили русскую науку.

№ слайда 4

Описание слайда:

Разбор софизмов прежде всего развивает логическое мышление, то есть прививает навыки правильного мышления. Обнаружить ошибку – это значит осознать её, а осознание ошибки предупреждает от повторения её в других математических рассуждениях. Что особенно важно, разбор софизмов помогает сознательному усвоению изучаемого материала, развивает наблюдательность, вдумчивость и критическое отношение к тому, что изучается. Математические софизмы приучают внимательно и настороженно продвигаться вперёд, тщательно следить за точностью формулировок, правильностью записей и чертежей, за допустимостью обобщений. Всё это нужно и важно. Наконец, разбор софизмов увлекателен. Чем труднее софизм, тем большее удовлетворение доставляет его анализ. Чем полезны софизмы и что они дают?

№ слайда 5

Описание слайда:

№ слайда 6

Описание слайда:

Алгебраические софизмы Вот некоторые результаты решения софизмов: (для подробного просмотра нажмите на выбранную строку) Пример 1.1 р. = 10 000 к. Пример 2.5 = 6 Пример 3.4 = 8 Пример 4.2 · 2 = 5 Пример 5.5 = 1 Пример 6.4 = 5 Пример 7.Любое число равно его половине Пример 8.Расстояние от Земли до Солнца равно толщине волоска Пример 9.Любое число = 0 Пример 10.Из двух неравных чисел первое всегда больше второго

№ слайда 7

Описание слайда:

Пример 1.1 р. = 10 000 к. Возьмём верное равенство: 1 р. = 100 к. Возведём его по частям в квадрат. Мы получим: 1 р. = 10 000 к.************************************************************************************Вопрос: В чём ошибка?Ответ (нажмите «Enter»): Возведение в квадрат величин не имеет смысла. В квадрат возводятся только числа.

№ слайда 8

Описание слайда:

Попытаемся доказать, что 5 = 6. С этой целью возьмём числовое тождество: 35 + 10 – 45 = 42 + 12 – 54. Вынесем общие множители левой и правой частей за скобки. Получим: 5 (7 + 2 – 9) = 6 (7 + 2 – 9). Разделим обе части этого равенства на общий множитель (заключённый в скобки).Получаем 5 = 6.************************************************************************************Вопрос: В чём ошибка?Ответ (нажмите «Enter»): Общий множитель (7 + 2 – 9) равен 0, а делить на 0 нельзя.

№ слайда 9

Описание слайда:

№ слайда 10

Описание слайда:

Пример 4.2 · 2 = 5 Имеем числовое равенство (верное): 4: 4 = 5: 5. Вынесем за скобки в каждой части его общий множитель. Получим: 4 (1: 1) = 5 (1: 1).Числа в скобках равны, поэтому 4 = 5, или 2 · 2 = 5.************************************************************************************Вопрос: Где здесь ошибка?Ответ (нажмите «Enter»): Ошибка допущена в вынесении общего множителя за скобки в левой и правой частях тождества 4: 4 = 5: 5.

№ слайда 11

Описание слайда:

Из чисел 5 и 1 по отдельности вычтем одно и то же число 3.Получим числа 2 и – 2. При возведении в квадрат этих чисел получаются равные числа 4 И 4. Значит, должны быть равны и исходные числа 5 и 1. ************************************************************************************Вопрос: В чём ошибка?Ответ (нажмите «Enter»): Из равенства квадратов двух чисел не следует, что сами эти числа равны.

№ слайда 12

Описание слайда:

Имеем числовое равенство (верное):16 – 36 = 25 – 45; 16 – 36 + 20,25 = 25 – 45 + 20,25;(4 – 4,5)2 = (5 – 4,5)2; 4 – 4,5 = 5 – 4,5; 4 = 5. ************************************************************************************Вопрос: В чём ошибка?Ответ (нажмите «Enter»): (4 – 4,5)2 = (5 – 4,5)2 ↔ |4 – 4,5| = |5 – 4,5|. Пример 6.4 = 5

№ слайда 13

Описание слайда:

Пример 7.Любое число равно его половине Возьмём два равных числа a и b, a = b. Обе части этого равенства умножим на a и затем вычтем из произведений по b2. Получим:a2 – b2 = ab – b2, или (a + b) (a – b) = b (a – b).Отсюда a + b = b, или a + a = a, так как b = a.Значит, 2a = a, a = . ************************************************************************************Вопрос: В чём ошибка?Ответ (нажмите «Enter»): Нельзя делить на (a – b), так как (a – b) = 0.

№ слайда 14

Описание слайда:

Пример 8.Расстояние от Земли до Солнца равно толщине волоска Пусть a (м) – расстояние от Земли до Солнца, а b (м) – толщина волоска. Среднее арифметическое их обозначим через v. Имеем:a + b = 2v, a = 2v – b, a – 2v = – b. Перемножив по частям два последних равенства, получаем:a2 – 2av = b2 – 2bv. Прибавим к каждой части v2. Получим:a2 – 2av + v2 = b2 – 2bv + v2, или (a – v)2 = (b – v)2, т.е. (a – v) = (b – v), и, значит, a = b. ************************************************************************************Вопрос: Где здесь ошибка?Ответ (нажмите «Enter»): Ошибка как в примере №6.

№ слайда 15

Описание слайда:

Пример 9.Любое число = 0 Каково бы ни было число a, верны равенства:(+a)2 = a2 и (– a)2 = a2. Следовательно, (+a)2 = (– a)2, а значит, +a = – a, или 2a = 0, и поэтому a = 0. ************************************************************************************Вопрос: В чём ошибка?Ответ (нажмите «Enter»):

№ слайда 16

Описание слайда:

Пример 10.Из двух неравных чисел первое всегда больше второго Пусть a и b – произвольные числа и a ≠ b. Имеем:(a – b)2 > 0, т.е. a2 – 2ab – b2 > 0, или a2 + b2 > 2ab.К обеим частям этого неравенства прибавим – 2b2. Получим:a2 – b2 > 2ab – 2b2, или (a + b) (a – b) > 2b (a – b). После деления обеих частей на (a – b) имеем:a + b > 2b, откуда следует, что a > b. ************************************************************************************Вопрос: Где допущена ошибка?Ответ (нажмите «Enter»): При делении обеих частей неравенства (a + b) (a – b) > 2b (a – b) на (a – b) знак неравенства может измениться на противоположный (если a – b < 0).

№ слайда 17

Описание слайда:

Геометрические софизмы Вот некоторые примеры геометрических софизмов: (для подробного просмотра нажмите на выбранную строку) Пример 1.Загадочное исчезновение. Пример 2.Земля и апельсин Пример 4.Два перпендикуляра Пример 5.«Новое доказательство» теоремы Пифагора

№ слайда 18

Описание слайда:

Пример 1.Загадочное исчезновение У нас есть произвольный прямоугольник, на котором начерчено 13 одинаковых линий на равном расстоянии друг от друга, так, как показано на рисунке 1. Теперь «разрежем» прямоугольник прямой MN, проходящей через верхний конец первой и нижний конец последней линии. Сдвигаем обе половины вдоль по этой линии и замечаем, что линий вместо 13 стало 12. Одна линия исчезла бесследно. ************************************************************************************Вопрос: Куда исчезла 13-я линия?Ответ (нажмите «Enter»):

№ слайда 19

Описание слайда:

Пример 2.Земля и апельсин Вообразим, что земной шар обтянут по экватору обручем и что подобным же образом обтянут и апельсин по его большому кругу. Далее вообразим, что окружность каждого обруча удлинилась на 1м. Тогда обручи отстанут от поверхности тел и образуют некоторый зазор************************************************************************************Вопрос: Где зазор будет больше: у апельсина или у Земли?Ответ (нажмите «Enter»): Пусть длина окружности земного шара = C, а апельсина с метрам. Тогда радиус Земли R = C/2 и радиус апельсина r = c/2 . После прибавки к радиусам 1 метра окружность обруча у Земли будет C + 1, а у апельсина c + 1. Радиусы их соответственно будут: (C + 1)/2 и (c + 1)/2 . Если из новых радиусов вычтем прежние, то получим в обоих случаях одно и то же.(C + 1)/2 - C/2 = 1/2 - для Земли, (c + 1)/2 - c/2 = 1/2 - для апельсина Итак, у Земли и у апельсина получается один и тот же зазор в 1/2 метра (примерно 16 см).

№ слайда 20

Описание слайда:

В дне деревянного судна во время плавания случилась прямоугольная пробоина в 13 см длины и 5 см ширины, т.е. площадь пробоины = 65 см2. Судовой плотник взял квадратную дощечку со стороной квадрата 8 см (т.е. площадь = 64 см2), разрезал её прямыми линиями на четыре части A, B, C, D так, как показано на рисунке 2, а затем сложил их так, что получился прямоугольник, как раз соответствующий пробоине, см. рисунок 3. Этим прямоугольником он и заделал пробоину. Вышло, что плотник сумел квадрат в 64 см2 обратить в прямоугольник с площадью 65 см2.*******************************************************Вопрос: Как такое могло получиться?Ответ (нажмите «Enter»): Легко видеть, что получившиеся при разрезании квадрата треугольники A и B равны между собой. Также равны и трапеции C, D. Меньшее основание трапеций и меньший катет треугольников равны 3 см и поэтому должны совпасть при совмещении треугольника A с трапецией C и треугольника B с трапецией D. В чём же секрет? Дело в том, что точки G, H, E не лежат на одной прямой, tg EHK = 8/3 , а tg HGJ = 5/2. Так как 8/3 – 5/2 = 1/6 > 0, то EHK > HGJ. Точно так же линия EFG – ломанная. Площадь полученного прямоугольника действительно равна 65 см2, но в нём имеется щель в виде параллелограмма, площадь которого в точности равна 1 см2. Наибольшая ширина щели равна 5 – 3 – (5·3)/8 = 1/8 см. Таким образом плотнику всё равно придётся замазывать небольшую щель.

№ слайда 21

Описание слайда:

Пример 4. Два перпендикуляра Попытаемся «доказать», что через точку, лежащую вне прямой, к этой прямой можно провести два перпендикуляра. С этой целью возьмём треугольник ABC (рисунок 4). На сторонах AB и BC этого треугольника, как на диаметрах, построим полуокружности. Пусть эти полуокружности пересекаются со стороной AC в точках E и D. Соединим точки E и D прямыми с точкой B. Угол AEB прямой, как вписанный, опирающийся на диаметр; угол BDC также прямой. Следовательно, BE AC и BD AC. Через точку B проходят два перпендикуляра к прямой AC. ****************************************************Вопрос: В чём ошибка?Ответ (нажмите «Enter»): Рассуждения опирались на ошибочный чертёж. В действительности полуокружности пересекаются со стороной AC в одной точке, т.е. BE совпадает с BD.

Описание слайда:

«Аванта +. Математика». – Москва, изд. «Аванта +»,1998.«БЭКМ – 2007». – Москва, 2007. Игнатьев Е.И. «Математическая смекалка. Занимательные задачи, игры, фокусы, парадоксы». – Москва, изд. «Омега»,1994.Нагибин Ф.Ф., Канин Е.С. «Математическая шкатулка». – Москва, изд. «Просвещение»,1988.

Cлайд 1

Математические софизмы Презентацию сделала ученица 7 класса Верхеиндырчинской основной школы Фатыхова Аделя

Cлайд 2

Введение История математики полна неожиданных и интересных софизмов и парадоксов. И зачастую именно их разрешение служило толчком к новым открытиям, из которых в свою очередь произрастали новые софизмы и парадоксы. В истории развития математики софизмы играли существенную роль.

Cлайд 3

Они способствовали повышению строгости в математических рассуждениях и содействовали более глубокому уяснению понятий и методов математики. Роль софизмов в развитии математики сходна с той ролью, какую играли непреднамеренные ошибки в математических доказательствах, допускаемые даже выдающимися математиками. Большинство софизмов известно очень давно, и можно найти в различных сборниках, журналах. Некоторые из них передаются устно из поколения в поколение.

Cлайд 4

Понятие «Софизм» Софизм – (от греческого sophisma , «мастерство, умение, хитрая выдумка, уловка») - умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям. Софизм основан на преднамеренном, сознательном нарушении правил логики. Каким бы ни был софизм, он всегда содержит одну или несколько замаскированных ошибок.

Cлайд 5

Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. Очень часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если их не понимать.

Cлайд 6

Cлайд 7

Экскурс в Историю Софизмы появились еще в Древней Греции. Они тесно связаны с философской деятельностью софистов - платных учителей мудрости, учивших всех желающих философии, логике и, особенно, риторике (науке и искусству красноречия). Наиболее известна деятельность старших софистов, к которым относят Протагора из Абдеры, Горгия из Леонтип, Гиппия из Элиды и Продика из Кеоса. Одна из основных задач софистов заключалась в том, чтобы научить человека доказывать (подтверждать или опровергать) все, что угодно, выходить победителем из любого интеллектуального состязания. Для этого они разрабатывали разнообразные логические, риторические и психологические приемы.

Cлайд 8

К логическим приемам нечестного, но удачного ведения дискуссии и относятся софизмы. Однако, одних только софизмов для победы в любом споре недостаточно. Ведь если объективная истина окажется не на стороне спорящего, то он, в любом случае, проиграет полемику, несмотря на все свое софистическое искусство. Это хорошо понимали и сами софисты. Поэтому помимо различных логических, риторических и психологических уловок в их арсенале была важная философская идея (особенно дорогая для них), состоявшая в том, что никакой объективной истины не существует: сколько людей, столько и истин. Софисты утверждали, что все в мире субъективно и относительно. Если признать эту идею справедливой, то тогда софистического искусства будет вполне достаточно для победы в любой дискуссии: побеждает не тот, кто находится на стороне истины, а тот, кто лучше владеет приемами полемики.

Cлайд 9

Аристотель называл софизмом «мнимые доказательства »,в которых обоснованность заключения кажущаяся и обязана чисто субъективному впечатлению, вызванному недостаточностью логического анализа. Убедительность на первый взгляд многих софизмов, их «логичность» обычно связана с хорошо замаскированной ошибкой - семиотической: за счёт метафоричности речи, нарушающих однозначность мысли и приводящих к смешению значений терминов, или же логической: подмена основной мысли (тезиса) доказательства, принятие ложных посылок за истинные, несоблюдение допустимых способов рассуждения (правил логического вывода), использование «неразрешённых» или даже «запрещённых» правил или действий, например деления на нуль в математических софизмах.

Cлайд 10

Исторически с понятием «софизм» неизменно связывают идею о намеренной фальсификации, руководствуясь признанием Протагора, что задача софиста (софист, от греч. sophistes - умелец, изобретатель, мудрец, лжемудрец) - представить наихудший аргумент как наилучший путём хитроумных уловок в речи, в рассуждении, заботясь не об истине, а об успехе в споре или о практической выгоде. С этой же идеей обычно связывают «критерий основания», сформулированный Протагором: мнение человека есть мера истины.

Cлайд 11

Алгебраические софизмы. Алгебра - один из больших разделов математики, принадлежащий наряду с арифметикой и геометрией к числу старейших ветвей этой науки. Задачи, а также методы, отличающие её от других отраслей математики, создавались постепенно, начиная с древности. Алгебра возникла под влиянием нужд общественной практики, в результате поисков общих приёмов для решения однотипных арифметических задач. Приёмы эти заключаются обычно в составлении и решении уравнений. Т.е. алгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях.

Cлайд 12

Итак у меня есть к вам и к себе интересная задачка для разминки ума... ...используя простейшие математические преобразования и формулы всем нам известные со школы, я могу доказать, что, при условии a=b+c "a" расняется "c" ...не верите?! смотрите: a=b+с Умножим обе части на a-b a2-ab=ab+ac-b2-bc Переносим ac в левую часть a2-ab-ac =ab-b2-bc Разложим на множители a(a-b-c)=b(a-b-c) Разделим обе части на a-b-c Получаем: a=b

Cлайд 13

Четыре ученицы – Мария, Нина, Ольга и Поля – участвовали в лыжных соревнованиях и заняли 4 первых места. На вопрос, кто какое место занял, они дали три разных ответа: 1) Ольга заняла 1-е место, Нина – 2-е, 2) Ольга – 2-е, Поля – 3-е, 3) Мария - 2-е, Поля – 4-е. Отвечавшие при этом признали, что одно из высказываний каждого ответа верно, а другое неверно. Какое место заняла каждая из учениц?

Cлайд 14

Решение. На рисунках 1 и 2 точки «верхнего» множества соответствуют именам учениц, а «нижнего» - занятым местам. Сплошные отрезки соответствуют высказываниям первой ученицы, штриховые – второй, штрихпунктирные – третьей. Отрезки, соответствующие ложному высказыванию, будем перечеркивать. Предположим, что Нина заняла второе место. В таком случае (рис. 1) Поля заняла третье и четвертое места, что по условию задачи невозможно. Предположим, что Оля заняла 1-е место (рис. 2), тогда Мария заняла 2-е место, Поля - 3-е место, Нина – 4-е.

Cлайд 15

Заключение. О математических софизмах можно говорить бесконечно много, как и о математике в целом. Изо дня в день рождаются новые парадоксы, некоторые из них останутся в истории, а некоторые просуществуют один день. Софизмы есть смесь философии и математики, которая не только помогает развивать логику и искать ошибку в рассуждениях. Буквально вспомнив, кто же такие были софисты, можно понять, что основной задачей было постижение философии. Но тем не менее, в нашем современном мире, если и находятся люди, которым интересны софизмы, в особенности математические, то они изучают их как явление только со стороны математики, чтобы улучшить навыки правильности и логичности рассуждений.

Cлайд 16

Понять софизм как таковой (решить его и найти ошибку) получается не сразу. Требуются определенный навык и смекалка. Некоторые софизмы приходилось разбирать по нескольку раз, чтобы действительно в них разобраться, некоторые же наоборот, казались очень простыми. Развитая логика мышления поможет не только в решении каких-нибудь математических задач, но еще может пригодиться в жизни. Мы поняли, что софистика-это целая наука, а именно математические софизмы - это лишь часть одного большого течения. Исследовать софизмы действительно очень интересно и необычно. Порой сам попадаешься на уловки софиста, на столь безукоризненность его рассуждений. Перед тобой открывается какой-то особый мир рассуждений, которые поистине кажутся верными. Благодаря софизмам и парадоксам можно научится искать ошибки в рассуждениях других, научится грамотно строить свои рассуждения и логические объяснения.

Cлайд 17

Литература 1. Lietzman W. Wo steckt der Fehler? Mathematische Trugschlüsse und Warnzeichen. – Leipzig? 1952 2. Аменицкий Н. Математические развлечения и любопытные приемы мышления. – М., 1912 3. Богомолов С. А. Актуальная бесконечность. – М.; Л., 1934 4. Больцано Б. Парадоксы бесконечного. – Одесса, 1911 5. Брадис В. М., Харчева А. К. Ошибки в математических рассуждениях. – М., 1938 6. Горячев Д. Н., Воронец А. М. Задачи, вопросы и софизмы для любителей математики. – М., 1903 7. Литцман В., Трир Ф. Где ошибка? – СПб., 1919 8. Лямин А. А. Математические парадоксы и интересные задачи. – М., 1911 9. Мадера А.Г., Мадера Д.А. Математические софизмы. – М.: Просвещение, 2003 10. Обреимов В. И. Математические софизмы. – 2-е изд. – СПб., 1889.

СодержаниеВведение
Древние софизмы
Числовые софизмы
Геометрические софизмы
Выводы

Что такое софизм?

Софизм (от греческого sophismaуловка, выдумка, головоломка)- логически
неправильное рассуждение, выдаваемое
за правильное.
Математический софизм- удивительное
утверждение, в доказательстве которого
кроются незаметные, а подчас и довольно
тонкие ошибки.
Эффектная демонстрация явно
неверного доказательства- в этом и
состоит смысл софизма.

Древние софизмы

Где появились софизмы?
В Древней Греции.
Для чего они создавались? С какой
целью?
Появление софизмов заставило
задуматься математиков о
логическом строении геометрии и
арифметики.
Кто придумал математические софизмы?
мудрец Зенон Элейский
в V веке до нашей эры.

Древние софизмы

Древний софизм «Рогатый»
Равен ли полный стакан пустому
Последние годы нашей жизни короче,
чем первые.

Древний софизм «Рогатый»

То, что ты не потерял, то и
имеешь. Ты не потерял рога,
следовательно, ты их имеешь.
Где ошибка?
ответ

Равен ли полный стакан пустому?

Оказывается, что да.
Пусть есть стакан, наполненный водой до
половины.
Тогда стакан, наполовину полный, равен стакану,
наполовину пустому.
Увеличим обе части равенства вдвое, получим, что
стакан полный равен стакану пустому.
=
Где ошибка?
ответ

Последние годы нашей жизни короче, чем первые

Известно изречение: в молодости идет время
медленнее, а в старости скорее. Это изречение
можно доказать математически.
Человек в течение тридцатого года жизни
проживает 1/30 часть своей жизни, в течение
семидесятого -1/70 часть жизни. Очевидно, что
1/30>1/70. Откуда ясно, что последние годы
жизни короче первых.
Не подвела ли математика?
ответ

Числовые софизмы

2=3
5=6
2·2=5
1=0, или уравнение x-a=0
не имеет решения

2=3

Рассмотрим очевидное равенство:
(2-5/2)2=(3-5/2)2
Тогда
(2-5/2)=(3-5/2)
Прибавив к обеим частям равенства по 5/2,
получим
2=3
Где ошибка?
ответы

5=6

Возьмем тождество:
35+10-45=42+12-54
Вынесем за скобки общий
множитель:
5·(7+2-9)=6·(7+2-9)
Разделим обе части на (7+2-9)
Получим 5=6
ответ

2·2=5

Напишем тождество:
4:4=5:5
Вынесем в каждой части общие
множители за скобки:
4·(1:1)=5·(1:1)
Так как 1:1=1, то 4=5, или
2·2=5
ответ

1=0, или уравнение х-а=0 не имеет корней

Дано уравнение x-a=0
Имеем:
(X-A)
0
=
(X-A)
(X-A)
1=0
Так как это равенство неверное, то
исходное уравнение не имеет
корней.
ответ

Геометрические софизмы

Пусть ΔАВСпроизвольный.
Проведем биссектрису
угла В и серединный
перпендикуляр к
отрезку АС.
Точку их пересечения
обозначим М.
Т.к. MD- высота и
медиана в ΔАМС, то он
равнобедренный
и АМ=МС
А
В
м
D
С

Геометрические софизмы

Опустим из точки М
перпендикуляры МЕ и MF на
стороны АВ и ВС
соответственно.
Из равенства треугольников
ВЕМ и ВFМ следует, что
МЕ=MF, ВЕ=BF.
В
E
F
м
А
D
С

Геометрические софизмы

Следовательно,
прямоугольные
треугольники АМЕ и
CMF равны:
у них равны
гипотенузы (АМ и МС)
и катеты (ME и MF)
значит AE=CF.
Итак, АЕ=СF, BE=BF
Следует, что AB=BC.
Возник парадокс: все
треугольники
равнобедренные
В
E
F
м
А
D
C

Геометрические софизмы

Ошибка в чертеже. Правильный
чертеж:
В
E
А
F
D
M
С

Выводы:

1.
2.
3.
познакомились с понятием
математические софизмы;
научились искать замаскированные
ошибки;
осознали:
важность правильных, корректных
записей и чертежей
недопустимость выполнения запрещенных
действий
важность учета применимости теорем,
формул и правил.

Ответы «Рогатый»

Ошибка здесь состоит в неправильном
переходе от общего правила к частному
случаю, который этим правилом не
предусмотрен.
Действительно, то, что ты не потерял,
подразумевает под словом «то» - все,
что ты имеешь, и ясно, что в него не
включены «рога».
Поэтому заключение «ты имеешь рога»
неправомерно.
назад

«Равен ли полный стакан пустому»

Приведенное рассуждение
неверно, так как в нем
применяется неправильное
действие: увеличение вдвое. В
данной ситуации его
применение бессмысленно.
назад

Ответ. «Последние годы нашей жизни короче, чем первые»

Действительно, 1/30>1/40>1/50.
Но неверно утверждение, что в
течение тридцатого года человек
проживает 1/30 часть жизни, он
проживает 1/30 только той части
жизни, которую он к этому моменту
прожил, но именно части, а не всей
жизни. Нельзя сравнивать между
собой части различных отрезков
времени.
назад

2=3

Если (2-5/2)2=(3-5/2)2, то
правильным следствием
должно быть
Ι2-5/2Ι=Ι3-5/2Ι, откуда следует
Ι-½Ι=Ι½Ι,
а вовсе не равенство 2-5/2=3-5/2
назад

5=6

Ошибка допущена при делении
верного равенства
5·(7+2-9)=6·(7+2-9)
на число (7+2-9), равное нулю.
Этого делать нельзя.
Любое равенство можно делить
только на число,
отличное от нуля!
назад

2·2=5

4:4=5:5
4/4=5/5
Вынесем общие множители:
4·1/4=5·1/5
В результате у нас не образуется общий
множитель, а в предложенном
доказательстве он был получен
вследствие некорректных действий:
4:4=4·(1:1)
назад

Уравнение х-а=0 не имеет корней, или 1=0

Так как х-а – корень
уравнения, то разделив
на (х-а) обе части,
мы потеряли этот корень
и поэтому получили неверное
равенство 1=0.
назад

Тема занятия
«Математические софизмы»

Цель занятия:
Углубить знания по математике. Интересно и организованно проверить знания у присутствующих по математике.
2. Развивать логику, воображение, творчество.
3. Повлиять на познавательную активность коллег в сторону её интенсификации.

Софизм - доказательство ложного утверждения, причем ошибка в доказательстве искусно замаскирована

Софизм - слово греческого происхождения и в переводе означает головоломку, хитроумную выдумку. Математические софизмы являются примерами таких ошибок в математических рассуждениях, когда при очевидной неправильности результата ошибка, приводящая к нему, хорошо замаскирована.

К софизмам можно отнести доказательство того, что Ахиллес, бегущий в 10 раз быстрее черепахи, не сможет ее догнать.
Пусть черепаха на 100 м впереди Ахиллеса.
Тогда Ахиллес пробежит эти 100 м, черепаха будет впереди его на 10 м.
Пробежит Ахиллес эти 10 м, а черепаха окажется впереди на 1 м и т.д.
Расстояние между ними будет сокращаться, но никогда не обратится в нуль. Значит Ахиллес никогда не догонит черепаху

Софистами называют группу древнегреческих философов 4-5 вв. до н.э., достигших большого искусства в логике.
В истории математики софизмы
играли существенную роль, они способствовали более глубокому уяснению понятий и методов математики.

Академик Иван Петрович Павлов говорил, что «правильно понятая ошибка – это путь к откровению». Уяснение ошибок в математических рассуждениях часто содействовало развитию математики. В этом плане особенно поучительна история аксиомы Евклида о параллельных прямых.

Примеры
Если равны половины, то равны и целые.
Полуполное есть то же, что и полупустое, полное – то же самое, что и пустое

Найдите ошибки в следующих рассуждениях:
Задача № 1.
Четырежды четыре – двадцать пять.
Доказательство:
16:16=25:25
16 (1:1)=25(1:1)
4*4=25
Ответ: Ошибка заключается в том, что распределительный закон умножения автоматически переносится на деление, что неверно

Задача № 2
С руб.=10000 С коп.
Доказательство:
С руб. = 100 С коп.
1 руб. = 100 коп.
Ответ: Умножать С руб., на 1 рубль нельзя, так как никаких «квадратных рублей» и «квадратных копеек» не существует

Практическая задача
После нового года цена на товар повысились дважды на 20 %. На сколько процентов повысилась цена товар после двух последовательных повышений?
Решение: стоимость товара – а руб.
после 1 повышения - 1,2 а руб.
после 2 повышения – 1,44 а руб.
Вывод: цена на товар повысилась на 44 %.

Всякие два равенства можно почленно перемножить. Применим это утверждение к написанным выше равенствам, получим новые равенства
С руб. = 10000 С коп

Ответ: следует задать вопрос: «Вы живете в этом городе?»
Ответ: «Да» - независимо от того, кто отвечает – житель города А или житель города Б означает, что Вы находитесь в городе А. Ответ: «Нет» при любых условиях будет означать, что Вы находитесь в городе Б.

Логическая задача – шутка:
Два города А и Б расположены рядом. Жители обоих городов часто навещают друг друга. Известно, что все жители города А всегда говорят только правду, а жители города Б всегда лгут.
Какой вопрос следует задать жителю, которого Вы встречаете в одном из городов (Вы не знаете в каком), чтобы по его ответу «Да» или «Нет» можно было сразу определить в каком городе Вы находитесь.

Математические софизмы могут быть очень полезны. Разбор софизмов развивает логическое мышление, помогает сознательному усвоению обучаемого материала, воспитывает вдумчивость, наблюдательность, критическое отношение к тому, что изучается. Кроме того, разбор софизмов увлекателен. Учащиеся с большим интересом воспринимают софизмы, и, чем труднее софизм, тем больше удовлетворение доставляет его разбор.

Особенно интересно эта работа может быть поставлена на дополнительных занятия учащихся старших классов. Знания по математике в начальном и среднем звене еще невелики. Однако на дополнительных занятиях можно познакомить учащихся с несложными математическими софизмами, основанными на нарушении законов действия. При этом, если учесть, что учащиеся начальной и средней школы склонны эмоционально реагировать на абсурдность утверждений, прочность усвоения математического факта значительно повышается

В педагогическом плане математические софизмы должны использоваться не столько для предупреждения ошибок, сколько для проверки степени сознательности усвоения материала. Начинать надо с самых простых софизмов, доступных пониманию учащихся, постепенно усложняя задачи по мере накопления учащимися математических знаний.
(кликните на картинке)